Assignment 5: Hough Transforms
This assignment dealt with the use of the Hough Transforms to detect straight lines and circles in edge detected images. The edge detection was performed using the Sobel operator and applying a threshold. The resultant binary image was used to compute the Hough Transform. Edge detection was also done using direction info and applied to both, the lines and the circles case.
Source Code:Detecting lines using hough transforms
The equation of a line in polar coordinates is the following:r = x*cos(theta) + y*sin(theta);With the given edge pixels (x and y coordinates), we can plot a corresponding curve in the (r, theta) space by varying theta from 0 to 360. Multiple intersections of these curves in the Hough Space is indicative of collinear points in the real space. This fact is utilized to draw edge lines by picking local maximas in the Hough Space.

Hough Transform of lax.pgm
 Original Image |
 Detected lines |
 Superimposed lines (thresh = 12) |
 Original Image |
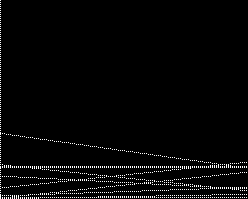 Detected lines |
 Superimposed lines |
Since we are dealing with discrete space, we must take into account the fact that the curves in the Hough Space may not intersect exactly at one pixel. So we check a 9x9 window and draw a line corresponding only to the maxima.
Effect of various gradient thresholds
 threshold = 6 |
 threshold = 20 |
 threshold = 30 |
The best result is obtained at a threshold of 12 as seen in the first set of images. At greater thresholds, we get rid of most of the edges, so even a small number of noise pixels that happen to line up will be picked up by the Hough Transform. The resultant lines do not appear to correspond to any real edges in the above images.
Detecting circles using hough transforms
Hough transforms can be used to detect circles in an image in a manner very similar to line detection. The equation of a circle is :
(x-a)2 + (y-b)2 = r2
where (a,b) is the center of the image and r is the radius. By plotting its Hough Transform in (a,b,r) space and picking out local maximas, we can find circles in the original image. This technique also requires edge detected image as the input.
Below are test cases with clear circles. The Hough Transform performs well only with the right set of parameters. For the examples below, a gradient threshold of 25 was picked, a threshold of 0.6*max_accum for the Hough Space, and a 9x9x9 neighborhood was checked for local maximas.
 Original image |
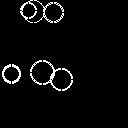 Detected circles |
 Superimposed circles |
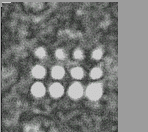 Original image |
 Detected circles |
 Superimposed circles |
Using direction info
Using the direction information for detecting edges may be a good idea if we have some prior knowledge of the image. For example, if we wanted to detect lines along the smaller walls of the buildings in lax.pgm, we could use a direction of 10 degrees to eliminate all pixels except those we are interested in. A hough transform would then show just the lines that line up with these walls.

This trick does not work well in the case of circles. Circles have edges in all directions and applying a direction threshold will only eliminate the pixels we are interested in. An example of this is shown below. Notice that none of the circles seem to align at the right place.

Conclusion:
Hough Transforms have high space and time complexities. For lines, the time complexity is O(N3) and for circles - O(N4). We can speed up circle detection by limiting the radius to a certain range that we are interested in. For line detection, theta can be incremented in intervals of 2 or more, thus speeding up the computation and reducing the memory requirements.
An improvement in results can be achieved by allowing only pixels with other edge pixels in its neighborhood to contribute to the Hough Space. By doing this, we can prevent stray noise pixels from contributing to lines or circles. Median smoothing after the Sobel operator has been applied can also bring about the same effect.